- MOOC(Massive Open Online Course)는 언제 어디서나 누구나 원하는 강의를 무료로 들을 수 있는 온라인 공개 강좌 서비스다. 2012년 미국에서 첫선을 보였고, 한국에선 2015년 10월 ‘K-MOOC’로 탄생했다. 올해 7월 현재 K-MOOC 수강신청자는 11만 명에 달할 정도로 인기가 높다(국가평생교육진흥원 K-MOOC 홈페이지 : www.kmooc.kr). ‘신동아’는 이번 호부터 K-MOOC 인기 강좌를 지면으로 옮겨 소개한다.

최적해, 절충해
배를 예로 들어보겠습니다. 배가 풍랑이나 파도에 전복되지 않으려면 선체가 넓어야 되죠. 선체가 넓으면 파도가 치고 바람이 불더라도 뒤집히지 않고 안정적으로 나아갈 수 있습니다. 그런데 문제는, 선체가 넓으면 물의 저항 때문에 속도를 잘 못 낸다는 거예요. 쾌속정같이 뾰족하게 생긴 배는 물의 저항을 적게 받아서 속도를 낼 수 있어요. 배의 안전성을 높이려니 속도가 떨어지고, 속도를 높이려니 안전성이 떨어지는 이러한 상황을 ‘기술적인 모순’이라고 하는데, 이런 모순이 들어 있는 문제를 ‘발명적 문제(Inventive Problem)’라고 해요.어느 하나를 좋게 하면 다른 하나가 희생된다는 건데, 이런 상황에서 해결책을 내라고 하면 어떻게 해야 할까요. 다시 배를 예로 들어보죠. 대부분의 사람들은 선체를 너무 넓게도, 너무 좁게도 만들지 않고 적절한 중간선에서 해결책을 내죠. 이처럼 중간선에서 해결책을 내는 것을 흔히 ‘최적해(最適解, Optimal Solution)’라고 하는데, 이건 사실 양자를 고려해 최적의 균형점을 찾는 거죠. 그러니 최적해가 아니라 타협안, 즉 ‘절충해’죠. 영어로는 ‘Trade-off’이고요.
그런데 정말로 좋은 해결책은 중간에서 타협하는 것이 아니라 양쪽 문제를 모두 해결하는 겁니다. 배의 속도를 높이면서도 안전성까지 좋아질 때 우리는 그것을 ‘발명적인 해결책(Inventive Solution)’이라고 합니다. 이건 그야말로 혁신적인 해결책이죠.
혁신의 최적 지점
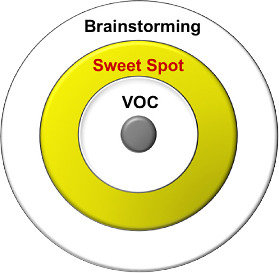
그런데 마케팅 분야에서는 고객의 목소리(VOC, Voice of the Customer)에 귀 기울이라고 많이들 얘기하죠. 그렇지만 고객은 뭔가 획기적인 해결책을 내는 게 아니에요. 현재 사용하면서 느끼는 작은 불편들을 이렇게 개선했으면 좋겠다는 이야기를 하지, 뭔가 혁신적인 해결책을 내진 못합니다.
스티브 잡스의 자서전에 이런 이야기가 나와요. 마차가 주요 운송수단이던 시기에 고객들한테 어떤 것을 원하느냐고 물었다면 “좀 더 힘이 센(마력이 강한) 마차를 원한다”는 식으로 대답하지, 자동차와 같은 혁신적인 수단을 생각해내진 못한다는 겁니다.
여러분께 쉽게 설명하면 양초나 호롱불을 켜던 시절에 고객들한테 “뭘 개선해드릴까요?” 하고 물으면 “호롱불의 그을음이 적게 나오면 좋겠다” “양초의 촛농이 적게 떨어지면 좋겠다” “조금 오래가는 양초, 조금 더 밝은 양초가 나왔으면 좋겠다”라고 답하지, 전깃불과 같은 것을 생각해내진 못한다는 얘기죠.
이처럼 브레인스토밍과 같이 자유분방하게 아이디어를 내라고 하면 현실과 떨어진 해결안들이 나오고, 고객의 목소리에 귀를 기울이면 현실과 너무 가까운 사소한 해결책이 나옵니다. 그러니까 큰 효과가 있으면서 실현 가능한 아이디어는 현실 문제에서 너무 가깝지도, 너무 멀지도 않은 중간 지점에서 나와야 한다는 건데요. 그걸 혁신의 Sweet Spot, 최적 지점이라고 합니다.
빈민가의 페트병 전등
이 같은 혁신의 최적 지점이 발명적 해결책이 되기 위한 두 가지 충분조건이 있다고 합니다. 이 두 가지 조건이 충족되면 100% 발명적인 해결책이 된다는 거죠. 첫 번째 조건은 ‘Closed World Condition’ 혹은 ‘CW Condition’, 우리말로 번역하자면 ‘닫힌 세계의 조건’이라는 겁니다. 두 번째 조건은 ‘Qualitative Change Condition’ 혹은 QC Condition, 즉 ‘질적 변화의 조건’입니다.닫힌 세계의 조건이라는 것은 해결책을 모색하는 데 내가 가진 여건, 내가 가진 자원 이외에 새로운 것을 집어넣지 말라는 겁니다. 닫힌 세계의 조건을 아주 잘 설명하는 예가 ‘적정기술’인 것 같은데요. 많이 들어봤죠? 우리는 무의식적으로, 기술이라는 것은 신기술이나 첨단기술이 좋다고 생각하는데요. 그 기술을 사용할 사회가 신기술이나 첨단기술을 구매할 수 있는 경제적 여력이 안 된다든지 또는 그 기술을 유지·관리할 수 있는 능력이 없으면 그 사회에 맞지 않는 기술이 됩니다. 그러니까 경제적으로 수용할 수 있고, 그 사회가 유지·관리할 수 있는 기술, 알맞은 기술, 즉 적정기술이 유용한 거죠.
많이 알려진 사례 중에 ‘물 1리터’가 아니라 ‘빛 1리터’라는 프로젝트(A Liter of Light Project)가 있습니다. 이 프로젝트는 필리핀의 빈민가에서 시작됐는데요. 빈민가니까 좁은 공간에 집을 다닥다닥 붙여서 지었어요. 전기가 들어오지 않고, 전기가 들어온다 해도 전기요금을 낼 능력이 없는 사람들이 살고요. 이런 빈민가는 대낮에도 집 안이 캄캄해요. 낮에도 집 안에 있지 못하고 집 밖으로 나와서 지내야 하는 형편입니다.
그래서 생각해낸 방법이 페트병입니다. 음료수 마시고 버린 페트병은 쓰레기통에서 얼마든지 찾을 수 있죠. 그 페트병에다가 물을 넣는 거예요. 물을 오랫동안 담아두면 녹조류 같은 것이 성장해서 물이 탁해지니까 그러지 못하도록 표백제를 조금 넣어요. 그러고는 지붕 위에 구멍을 뚫어 이 페트병을 꽂아놓는 겁니다. 그러면 이 페트병이 햇빛처럼 집안을 비춰주는 전등 노릇을 합니다. 유튜브에 있는 동영상 화면을 보시면 알 수 있어요.
자, 그런데 이 문제를 해결하면서 빈민가 사람들이 외부에서 다른 부품을 돈 주고 구매하고 조달하진 않았잖아요. 이런 상황을 ‘닫힌 세계의 조건’이라고 합니다. 닫힌 세계의 조건은 Innovation Sweet Spot의 관점에서 볼 때 아이디어가 현실 문제에서 가까워지게 할까요, 아니면 멀어지게 할까요. 닫힌 세계라는 것은 문제를 해결하기 위해서 내가 갖고 있지 않은 것을 가지고 오지 않죠. 있는 것만 가지고 해결하니까 문제의 해결책이 황당해지는 것을 방지하죠. 너무 멀리 가는 것을 방지하는 역할을 하는 겁니다.
발판 연결 바리케이드

SIT(Systematic Inventive Thinking)를 창안한 로니 호로위츠 박사는 저서에서 질적 변화의 조건을 설명하기 위해 바리케이드를 예로 들었어요. 자, 시위 하러 나온 군중이 허용된 구역 안에서 질서 있게 자기 의견을 표명할 수 있도록 바리케이드를 설치하면 문제가 생겨요. 시위 군중이 바리케이드를 밀면 미는 힘에 의해 바리케이드가 무너지죠. 그래서 ‘시위 군중이 늘어나도 바리케이드가 무너지지 않도록 하려면 어떻게 해야 하는가’ 하는 문제가 발생합니다.
이 문제를 기술적인 모순으로 설명하면, 문제를 악화시키는 요인은 ‘시위 군중의 수’입니다. 시위하러 나온 사람이 몇 명 안 될 때는 바리케이드를 밀어도 문제가 없는데, 시위 군중이 많아지면 바리케이드가 넘어지죠. 근원적인 해결 방법이 있을까요? 바리케이드를 2중으로 친다? 땅속 깊이 박는다? 그러면 비용, 시간, 노력이 많이 들어가죠. 그런 방법 말고는 군중의 수가 늘더라도 바리케이드가 쓰러지지 않게 할 방법이 없을까요? 굉장히 어려운 문제죠.
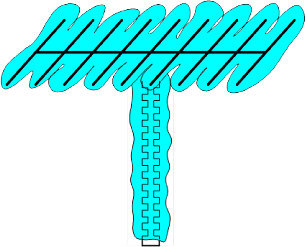
호로위츠 박사는 어떤 아이디어를 내놓았을까요. 간단하게 그림으로 그려봤는데, 바리케이드가 발판에 연결되도록 만드는 겁니다. 시위 군중의 수가 늘면 바리케이드의 발판을 밟고 있는 사람도 늘게 됩니다. 시위 군중의 수가 늘어나면 미는 힘도 늘어나지만, 발판을 지지하는 힘도 따라서 늘어날 테니 바리케이드가 넘어질 가능성은 더 커지지 않고 일정한 상태를 유지하죠. 모순을 근원적으로 해결했죠.
눈 쌓이는 안테나
다시 말해 ‘닫힌 세계의 조건(CW Condition)’은 해결책이 현실 문제와 너무 멀어지는 것을 억제하고, ‘질적 변화의 조건(QC Condition)’은 해결책이 현실 문제와 너무 가까워지는 걸 방지하고 바깥으로 밀어내는 역할을 하죠. 그래서 이 두 가지 조건이 충족되면 해결책이 혁신의 적당한 위치(Innovation Sweet Spot)에 오는 겁니다.
두 가지 조건이 모두 충족된 예를 하나 소개하겠습니다. 유럽의 어느 나라에서 군용 안테나를 납품하라는 입찰 공고를 냈는데, 조건이 뭐냐면 소수 인원이 이 안테나를 들고 적진에 잠입할 수 있어야 한다는 거예요. 그런데 한두 사람이 들고 갈 만큼 가벼워야지, 여러 사람이 들고 들어가면 발각될 가능성이 높잖아요. 또한 적진에 들어가 꽂아놓고 나오면 유지·보수할 필요가 없어야 돼요. 사람이 그거 고치러 들어갔다가 발각될 수 있으니까. 그리고 대량으로 납품받아야 되니까 가격이 싸야 해요. 이런 조건으로 군용 안테나를 납품할 업체를 모집했습니다.
그런데 유럽 산악지역의 일교차가 심하잖아요. 추운 날 밤 눈보라가 치면 눈이 안테나의 수신부에 쌓여 얼음이 되고 그 위에 눈이 오면 얼음이 점점 커집니다. 그렇게 수신부가 무거워지면 안테나가 부러집니다. 자, 이게 기술적인 모순이에요. 안테나 기둥이 안 부러지려면 굵게 만들거나 여러 개로 만들어야 하는데, 그러면 기둥이 무거워져서 한두 사람이 들고 갈 수가 없잖아요. 그렇다고 강도가 뛰어난 신소재를 쓰면 가격이 높아져 현실적으로 수용하기 힘들게 됩니다.
공모에 낙찰된 업체의 아이디어는 이랬습니다. 안테나 기둥에 요철을 만들어 눈이 오면 안테나 수신부에만 눈이 쌓이는 게 아니라 기둥에도 눈이 잘 달라붙도록 만들었어요. 수신부에 눈이 쌓여 얼음이 맺히면 안테나 기둥에도 눈이 쌓여 얼음이 맺혀요. 안테나 위가 무거워지면 기둥도 얼음에 둘러싸여 굵어지니까 튼튼해지죠.
재미있는 건, 수신부의 얼음이 녹으면 기둥에 있는 얼음도 녹는다는 거예요. 문제점을 유발하는 게 수신부에 생성되는 얼음인데, 해결책은 기둥에도 얼음이 생기도록 하는 것이죠. 문제가 발생하면, 즉 수신부에 얼음이 생기면 해결책이 작동해요. 기둥에도 얼음이 생기는 거죠. 날씨가 따뜻해 얼음이 쌓이지 않으면 기둥에도 얼음이 필요 없죠. 문제점을 해결책으로 이용할 뿐만 아니라, 필요할 때만 해결책이 나타나고 필요하지 않을 때는 없어지는 아주 이상적인 해결책입니다.
이렇게 쉬운 걸 왜 몰랐지?
이 해결책을 듣고 나면 많은 사람이 “어! 이렇게 쉬운 거를 나는 왜 생각 못했지?”라는 반응을 보입니다. 알고 보면 너무 쉬운데 생각해내려니까 너무 어려운 거예요. 그런데 혁신적인 해결책이 되기 위한 두 가지 조건, ‘닫힌 세계의 조건’과 ‘질적 변화의 조건’이 충족되는지를 보세요. 이 문제를 해결하기 위해 외부에서 어떤 새로운 자원을 가져오지 않았죠? 있는 상황을 그대로 이용했을 뿐 뭔가 새로운 것을 집어넣은 게 없으니 ‘닫힌 세계의 조건’이 충족되죠. 또한 안테나 수신부에 얼음이 많이 생겨도 안테나 기둥이 부러질 가능성이 더 커지지 않죠. 기둥을 둘러싼 얼음 기둥도 커지니까요. 질적 변화가 일어난 겁니다.자, 이 두 가지 조건이 적용된다면 얼마나 효과적인 해결책입니까. 그야말로 혁신적인 해결책, Innovation Sweet Spot 안에 들어 있는 해결책이죠. 이런 이야기를 듣고 보면 그런 해결책을 찾을 수 있는 능력을 기르는 방법이 없을까 하는 궁금증이 생기죠? 그래서 Systematic Inventive Thinking에서는 이러한 발명적인 해결책을 내는 데 도움이 되는 가이드라인을 제시했어요. 이를 ‘SIT의 5가지 사고도구’라고 합니다.
첫째, 뭔가를 더해서 해결하지 말고 가능하다면 있는 것 중에서 뭔가를 빼내서 해결하라는 겁니다. 그야말로 ‘닫힌 세계의 조건’을 강력하게 적용하는 거죠. 둘째, 하나의 요소가 2개 이상의 기능을 감당하도록 Task Unification(용도 통합)을 해보라는 겁니다. 셋째는 복제를 이용하라, 넷째는 분할을 이용하라, 다섯째는 속성 의존성을 이용하라는 겁니다.
박 영 택

● KAIST 박사(산업공학)
● 現 성균관대 시스템경영공 학과·기술경영전문대학원 교수, 한국품질경영학회 회장, 중국 칭화대 경제관리대학 객원교수
● 저서 : ‘박영택 창의발상론’ ‘박영택 품질경영론’






















![[지상중계] 제12회 나지포럼, “북미 정상회담 성과내기 어려워”](https://dimg.donga.com/a/380/211/95/1/ugc/CDB/SHINDONGA/Article/69/43/48/32/69434832107aa0a0a0a.jpg)
